Optimizing 3D Square Convolution for cuDNN-like Performance - A Worklog

18 Apr, 2025

Modern deep learning applications use convolution almost all the time, and guess what convolution is the heart of image processing. From adding gaussian blur and edge convolution to identifying temporal relation among frames in a T2V model, convolution is just everywhere which presents us the opportunity to optimize it for good.

In this worklog, we shall iteratively optimize 3D Square convolution in CUDA. All the benchmarks are on NVIDIA A100.

This worklog will be easy to understand if you have basic understanding of CUDA programming model, basics of convolution and a little bit of linear algebra.

Also this problem has been opted from Tensara. They have a pretty good set of kernels to test and benchmark your knowledge.

Full code for 3D Square Convolution is available on my Diffusion Kernels repo here: Diffusion Kernels

Let's get to the point!

The basics

Before diving deep into solving the kernel, lets touch some grass on 3D convolution between a input volume and a cubic kernel.

$C [i, j, k] = \sum_{x = 0}^{K - 1} \sum_{y = 0}^{K - 1} \sum_{z = 0}^{K - 1} A [i + x, j + y, k + z] \cdot B [x, y, z]$

Looks super complicated! NO its not, think of it like a 2D kernel where each element in the input matrix is getting to dot product with a 2D cubic kernel. Here we just extend the dimension by z or depth which essentially could imply depth or temporal dimension depending on the sort of problem you are solving.

$\frac{size - K + 2 P}{stride} = size$

stride is simply 1 here, hence;

$size - K + 2 P = size; P = \frac{K - 1}{2}$

Which means the kernel is centered at each position, with $\frac{K - 1}{2}$ elements on each side in all dimensions or to simply put the padding will be $\frac{K - 1}{2}$

Throughout this worklog we will be working on with float32 precision, which means I keep float8 and its optims for future which I shall talk at end.

For operations like convolutions, PyTorch internally uses cuDNN kernels. Lets see how much time it takes for a 512x512x512 tensor to get square convoluted to 9x9x9 kernel.

import time
import torch
import torch.nn as nn
import torch.backends.cudnn as cudnn

cudnn.enabled = True
print(f"cuDNN enabled: {torch.backends.cudnn.enabled}")

device = "cuda" if torch.cuda.is_available() else "cpu"
print(f"{device} available!")

conv3d = nn.Conv3d(
    in_channels=1,
    out_channels=1,
    kernel_size=9,
    stride=1,
    padding=4
).to(device)

input_tensor = torch.randn(1, 1, 512, 512, 512, device=device, dtype=torch.float32)

# Warm up pass
with torch.no_grad():
    _ = conv3d(input_tensor)
    torch.cuda.synchronize()

num_runs = 10
total_time = 0

for i in range(num_runs):
    torch.cuda.synchronize()
    start_time = time.time()

    output = conv3d(input_tensor)

    torch.cuda.synchronize()
    end_time = time.time()

    total_time += (end_time - start_time) * 1000

print(f"Input shape: {input_tensor.shape}")
print(f"Output shape: {output.shape}")
print(f"Average Execution time: {(total_time/10):.4f} ms")

So PyTorch takes around 147 ms to process a 512x512x512 shaped tensor. Hmm interesting, now before we move on to kernels let us check if our problem is memory bound or compute bound.

Let's calculate for a 3D convolution with these config as shown in PyTorch impl:

Input tensor A: 1×1×512×512×512
Kernel B: 1×1×9×9×9
Output tensor C: 1×1×512×512×512 (with padding=4)

Calculating FLOPs for 3D convolution

For each output element, we perform:

9×9×9 = 729 multiplications
728 additions (to sum the products) = 1,457 operations per output element

Total output elements: 512×512×512 = 134,217,728 Total FLOPs = 134,217,728 × 1,457 = 195,555,129,696 ≈ 195.6 GFLOPs

Calculating memory accesses

Read input tensor: 1×1×512×512×512 × 4 bytes = 536,870,912 bytes
Read kernel weights: 1×1×9×9×9 × 4 bytes = 2,916 bytes
Write output tensor: 1×1×512×512×512 × 4 bytes = 536,870,912 bytes

Total bytes transferred = 1,073,744,740 bytes ≈ 1.07 GB

Calculating arithmetic intensity

Arithmetic intensity = FLOPs / Bytes transferred = 195,555,129,696 / 1,073,744,740 ≈ 182.1 FLOPs/byte

Hence with an arithmetic intensity of approximately 182.1 FLOPs/byte, this 3D convolution is compute-bound, operations with ratios > 10-20 FLOPs/byte are typically compute-bound. In our case large kernel size (9×9×9) requires many arithmetic operations per output element.

Kernel 1: Naive 3D Square Conv

We can write a naive kernel for this in which each thread is responsible for calculating output element of the 3D matrix. The indexing would be simple in i, j and k'th dimension as so -

int i = blockIdx.x * blockDim.x + threadIdx.x;
int j = blockIdx.y * blockDim.y + threadIdx.y;
int k = blockIdx.z * blockDim.z + threadIdx.z;

if (i < size && j < size && k < size){
   float sum = 0.0f;

   for (int x = 0; x < K; x++){
       for (int y = 0; y < K; y++){
            for (int z=0; z < K; z++){
                 int iPos = i + (x - radius);
                 int jPos = j + (y - radius);
                 int kPos = k + (z - radius);

                 if (
                    iPos >= 0 && iPos < size && 
                    jPos >= 0 && jPos < size &&
                    kPos >= 0 && kPos < size
                 ){
                     sum += A[(iPos * size + jPos) * size + kPos] * B[(x * K + y) * K + z];
                  }
            }
        }
   }

   C[(i * size + j) * size + k] = sum; 
}

Running this naive kernel results in the following results -

Test Case: (D=H=W=512, K=9)
>> GPU allocation time: 1.063296 ms
>> Host to device transfer time: 138.113480 ms
------- 3D Convolution kernel ---------
>> Execution time: 666.605591 ms
>> Achieved (GFLOPS): 293.359711
---------------------------
>> Device to host transfer time: 302.634247 ms

Far from what claimed in the title of this blog :) Don't worry we will get there, lets move to next one!

Kernel 2 - Coalesced Global Access

Allow me to explain coalesced access with a simple diagram.

non-coalesced-mem-access

Inside GPU every Streaming Multiprocessors has some set of warp and every warp consists of 32 threads, these threads are responsible for executing single instruction at a time.

Essentially for CEIL(size * size * size, 256) blocks, every block contains CEIL(256, 32) warps. But what is the bottleneck here? Its the access pattern, every thread tries to access not consecutive but divergent memories in naive kernel which could be size or size x size apart.

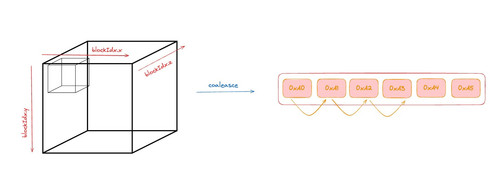
coalesced-mem-access

We fix this by computing contiguous output block elements specially which could be easily grouped by the memory controller so that the cache hits maximizes for L1/L2 caches. Though we can't directly access L1 or L2 cache but we could program our kernel such that it can coalesce the memory and maximize the cache hit.

And we do it like so,

int idx = blockIdx.x * blockDim.x + threadIdx.x;

if (idx < size * size * size){
    int k = idx % size;
    int j = (idx / size) % size;
    int i = idx / (size * size);

    # compute 3D Square Convolution in same way

    C[idx] = sum; # store in C
}

The fact to be noted is we are not only colaesing in k dimension but also j and i dimension such that every index is contiguous in its own way. Damn that was good, lets check the results!

Test Case: (D=H=W=512, K=9)
------- 1D Indexed Convolution Kernel ---------
>> Execution time: 115.665825 ms
>> Achieved (GFLOPS): 1690.691528
---------------------------
------- Performance Comparison ---------
>> 3D Kernel Time: 666.719238 ms
>> 1D Kernel Time: 115.665825 ms
>> Speedup (3D/1D): 5.764185
---------------------------
Results match between kernels: Yes

It might seem like we beat cuDNN on performance based on the execution time but nope, we didn't count for memory transfers. Also later I would write a cuDNN kernel myself from the actual cuDNN api to test and benchmark the results.

Kernel 3 - Vectorized float4 Loads

We are already coalescing the kernel then what else we could ponder in contiguous memory load space!? Lets think like this, we have this 4 instructions B[x + 0], B[x + 1], B[x + 2], B[x + 3], these instructions are 4 in total to fetch from L1/L2 cache or coalesced warp threads but what if it could be 1 instruction instead of 4. Yeah float 4 does exactly that.

float4 holds 4D coordinates in x, y, z and w plane, which is 16 bytes of data in FP32 precision. To use float4 we do it like so,

float4 kernelBWeights = *reinterpret_cast<const float4*>(&B[(x * K + y) * K + z]);

for (int zOffset = 0; zOffset < 4; zOffset++) {
    int iPos = i + (x - radius);
    int jPos = j + (y - radius);
    int kPos = k + (z + zOffset - radius);

    if (iPos >= 0 && iPos < size && 
        jPos >= 0 && jPos < size &&
        kPos >= 0 && kPos < size) {
        
        float weight;
        if (zOffset == 0) weight = kernelBWeights.x;
        else if (zOffset == 1) weight = kernelBWeights.y;
        else if (zOffset == 2) weight = kernelBWeights.z;
        else weight = kernelBWeights.w;
        
        sum += A[(iPos * size + jPos) * size + kPos] * weight;
    }
}

In my impl you would find that there is a mod operation done on K of 4 because if K isn't divisible by 4 the values cant't be loaded in vectorized fashion everytime for those K x K x K kernel.

Test Case: (D=H=W=512, K=9)
>> GPU allocation time: 0.958848 ms
>> Host to device transfer time: 109.603363 ms
------- Optimized 3D Convolution kernel ---------
>> Execution time: 120.711166 ms
>> Achieved (GFLOPS): 1620.026123
---------------------------
>> Device to host transfer time: 381.381195 ms

You might easily notice that the throughput has decreased instead of increasing for the test case. And there are several reasons for this. First is K, which is not divisible by 4 and hence it falls back to coalesced access, and since D increases drastically, there is a significant pressure on memory bandwidth and cache utilization. The A100 has limited L1/L2 cache space relative to this data size, causing more global memory accesses.

While I show you the output only for this particular case, the average GFLOPs achieved overall across different kernel and input volumes, is higher and is approx 1229 compared to an average of 1172 from the coalesced one, a good 5% improvement on FLOPs acheived.

Kernel 4 - Shared Mem and Tiling

My intuition was to move A into shared memory in tiles, though doing this means L1 cache becomes useless, since we access GMEM only via SMEM so we carve out all of L1 to SMEM. But it's good to do anyway since it gives more of a granularity on what MIO are we doing.

The idea here is simple, since we are not using special math instructions, nor dynamic branches, it’s clear that we’re stalling waiting for our SMEM accesses to return.

Which is a problem, and to counter it, we allow each thread to load multiple elements to fill the shared mem tile, now when you would see my code, it will be such that, I would have transformed the gridDim from 1D to 3D again, reason being I found the warp schedulers are able to manage it well with >1D dimension tiling and when I compared, it gives a little speed up about 2-3% (Remember this is not ONLY the SMEM caching that I'm comparing with but 1D and 3D gridDimension).

Before we move on to look at the impl, I would like to show you a simple derivation for TILE_WIDTH, what is the idea behind choosing it!

Understanding What Each Output Element Needs

In a 3D convolution, to compute one output value at position (i,j,k), we need a cube of input data centered on that position.

For a kernel of size K (e.g., K=3, K=5, etc.), we need to look at:

radius = (K-1)/2 elements in each direction from the center

For example, with K=3 (radius=1), to compute the output at position (i,j,k), we need input elements from:

i-1 to i+1 (3 elements)
j-1 to j+1 (3 elements)
k-1 to k+1 (3 elements)

Understanding What a Tile of Output Elements Needs

Now, imagine computing not just one output element, but a 3D block (tile) of output elements of size TILE_SIZE×TILE_SIZE×TILE_SIZE. Let's say this output tile starts at position (base_i, base_j, base_k) and ends at (base_i+TILE_SIZE-1, base_j+TILE_SIZE-1, base_k+TILE_SIZE-1).

The leftmost element in our output tile (at base_i) needs elements from (base_i-radius)
The rightmost element in our output tile (at base_i+TILE_SIZE-1) needs elements up to (base_i+TILE_SIZE-1+radius)

So in the i-dimension, we need input data from:

Starting point: base_i - radius
Ending point: base_i + TILE_SIZE - 1 + radius

The same logic applies to the j and k dimensions.

Calculating the Total Width Required

To find the total width of input data needed in each dimension:

Width = (Ending point - Starting point + 1)
      = (base_i + TILE_SIZE - 1 + radius) - (base_i - radius) + 1
      = base_i + TILE_SIZE - 1 + radius - base_i + radius + 1
      = TILE_SIZE - 1 + radius + radius + 1
      = TILE_SIZE + 2*radius

Now that we have cleared everything in theory, lets look at my last optim now :), here it goes,

extern __shared__ float tileA[];
    
    int tx = threadIdx.x % TILE_SIZE;
    int ty = (threadIdx.x / TILE_SIZE) % TILE_SIZE;
    int tz = threadIdx.x / (TILE_SIZE * TILE_SIZE);
    
    int base_i = blockIdx.x * TILE_SIZE;
    int base_j = blockIdx.y * TILE_SIZE;
    int base_k = blockIdx.z * TILE_SIZE;
    
    int i = base_i + tx;
    int j = base_j + ty;
    int k = base_k + tz;
    
    const int tile_width = TILE_SIZE + 2*MAX_RADIUS;
    const int tile_area = tile_width * tile_width;
    const int tile_volume = tile_area * tile_width;
    
    // Collaborative loading of input data into shared memory (including halo regions)
    // Each thread loads multiple elements to fill the shared memory tile
    for (int load_idx = threadIdx.x; load_idx < tile_volume; load_idx += blockDim.x) {
        int local_k = load_idx % tile_width;
        int local_j = (load_idx / tile_width) % tile_width;
        int local_i = load_idx / tile_area;
        
        int global_i = base_i + local_i - radius;
        int global_j = base_j + local_j - radius;
        int global_k = base_k + local_k - radius;
        
        if (global_i >= 0 && global_i < size &&
            global_j >= 0 && global_j < size &&
            global_k >= 0 && global_k < size) {
            tileA[local_i * tile_area + local_j * tile_width + local_k] = 
                A[(global_i * size + global_j) * size + global_k];
        } else {
            tileA[local_i * tile_area + local_j * tile_width + local_k] = 0.0f;
        }
    }
    
    // Ensuring all threads finish loading before computation
    __syncthreads();

Point to be noted here is we need to calculate thread volume since we are launching 3D grid and tile_A will store elements in 3D fashion.

Excited to see the result!? Yeah me too, lets check!

Test Case: (D=H=W=512, K=9)
>> GPU allocation time: 1.060928 ms
>> Host to device transfer time: 104.662880 ms
------- Tiled 3D Convolution kernel ---------
>> Execution time: 103.470078 ms
>> Achieved (GFLOPS): 1889.968872
---------------------------
>> Device to host transfer time: 309.049591 ms

We get a whopping 1889 GFLOPs on A100, pretty good, and the execution time is brought down to 103ms.

I tried to keep up with cuDNN till size 96 but it simply outperforms for size greater than 96. A long way to go to achieve 14k GFLOPs :)

=== Performance Summary ===
Size | Kernel | Custom Time | Custom GFLOPS | cuDNN Time | cuDNN GFLOPS | Speedup
--------------------------------------------------------------------------------
  64 |      3 |       0.03 ms |       420.06 |      0.80 ms |       17.34 |  24.22x
  96 |     11 |       1.25 ms |      1884.67 |      1.54 ms |     1528.76 |   1.23x
 256 |      7 |       6.30 ms |      1823.17 |      3.14 ms |     3658.45 |   0.50x
 512 |      9 |     103.38 ms |      1891.58 |     13.74 ms |    14236.34 |   0.13x

You can find all the code Diffusion Kernels, be sure to check this out and play around with TILE_SIZE and maybe doing more optims from here onwards!

References

Some images and intuitios of the optimisations have been taken from giga chads like Simon's and Maharshi's blogs.

Although I have much to digest from Pranjal's worklog too on Outperforming cuBLAS on H100.

Without these I won't have gotten so far.

Conclusion

If I get back to working on this Conv 3D square kernel, here are some optimizations I will look at next,

Warp tiling: where we could use different warps to execute instructions in parallel on different warp schedulers and concurrently on same warp scheduler.
Autotuning: with help of a bash script to do a grid search on all sensible combinations and benchmarks their runtime.
Tensor cores: with fp32 accum with mixed precision may help us increase throughput a lot as our 3D Square Conv is compute bound and not memory.

The full code is available on the GitHub repository: Diffusion Kernels

If you liked my worklog, make sure to follow me on X/twitter for more such awesome stuff!

See you in next banger post!